贝叶斯模型是机器学习中的一个重要分支,它依据贝叶斯定理,用于处理不确定性问题。贝叶斯模型能够用于分类、回归、聚类等多种使命。下面我将为您扼要介绍贝叶斯模型的基本原理和常用办法。
贝叶斯定理
贝叶斯定理是贝叶斯模型的中心,它描绘了在已知某些条件下,某个事情产生的概率。其公式为:
$$ P = frac{P cdot P}{P} $$
其间,$ P $ 表明在条件 B 下事情 A 产生的概率,$ P $ 表明在条件 A 下事情 B 产生的概率,$ P $ 和 $ P $ 别离表明事情 A 和 B 的先验概率。
贝叶斯分类器
贝叶斯分类器是一种依据贝叶斯定理的分类办法,它假定每个类别的特征散布是独立的。常用的贝叶斯分类器有:
1. 朴素贝叶斯分类器:假定每个特征之间彼此独立,适用于文本分类、垃圾邮件过滤等使命。2. 贝叶斯网络:也称为信仰网络,是一种图形化的贝叶斯模型,能够表明特征之间的依靠联系,适用于杂乱的联系建模。
贝叶斯回归
贝叶斯回归是一种依据贝叶斯定理的回归办法,它经过概率散布来表明模型的猜测成果。常用的贝叶斯回归办法有:
1. 高斯进程回归:运用高斯进程来表明模型的猜测散布,适用于非线性回归和函数迫临。2. 贝叶斯线性回归:将线性回归模型与贝叶斯办法结合,运用概率散布来表明模型的参数。
贝叶斯优化
贝叶斯优化是一种依据贝叶斯定理的优化办法,它经过构建概率模型来估量函数的值,并运用这些估量来辅导查找进程。贝叶斯优化常用于超参数调优、机器学习模型挑选等使命。
贝叶斯模型的优势
1. 处理不确定性:贝叶斯模型能够自然地处理不确定性问题,经过概率散布来表明模型的不确定性。2. 灵敏的模型挑选:贝叶斯模型能够轻松地扩展到不同的模型结构,经过调整模型参数来习惯不同的使命。3. 强壮的解说性:贝叶斯模型能够供给关于模型参数和猜测成果的概率解说,有助于了解模型的决议计划进程。
贝叶斯模型是机器学习中的一个重要分支,它依据贝叶斯定理,能够用于分类、回归、聚类等多种使命。贝叶斯模型具有处理不确定性、灵敏的模型挑选和强壮的解说性等优势。假如您对机器学习感兴趣,贝叶斯模型是一个值得深化研究的范畴。
深化解析机器学习中的贝叶斯模型
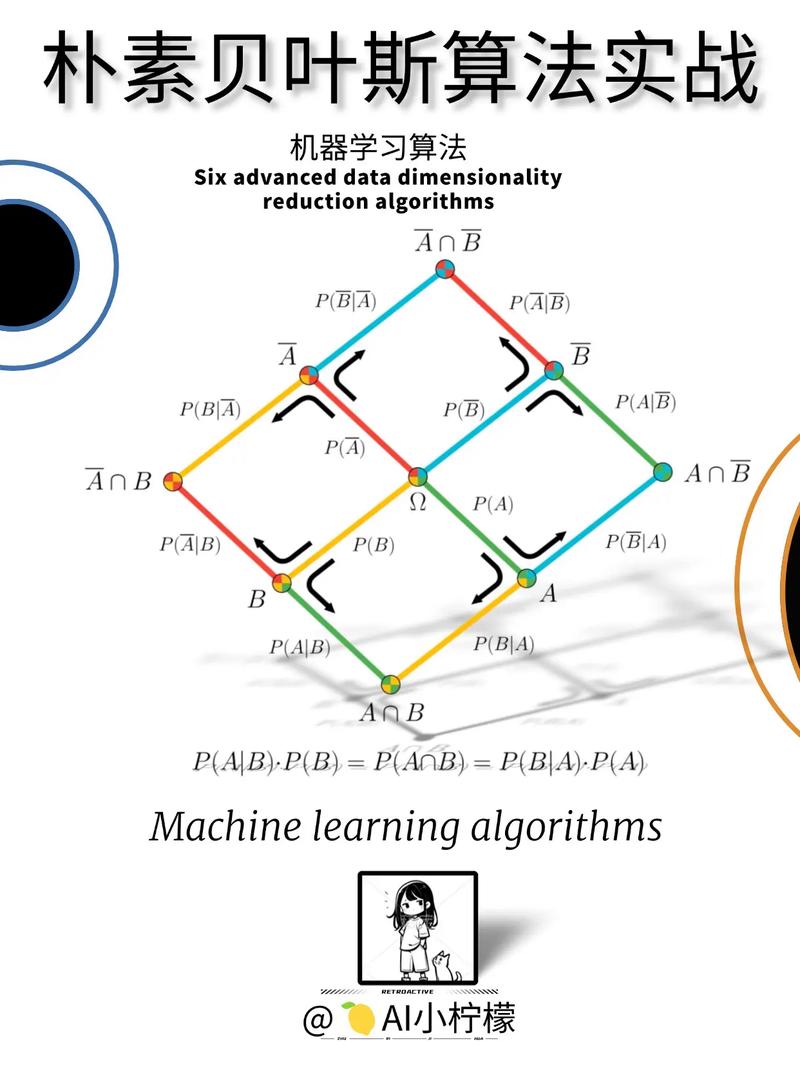
贝叶斯模型是机器学习中一种依据概率核算的强壮东西,尤其在分类和猜测使命中表现出色。本文将深化探讨贝叶斯模型的基本原理、使用场景以及其在机器学习中的重要性。
一、贝叶斯定理概述
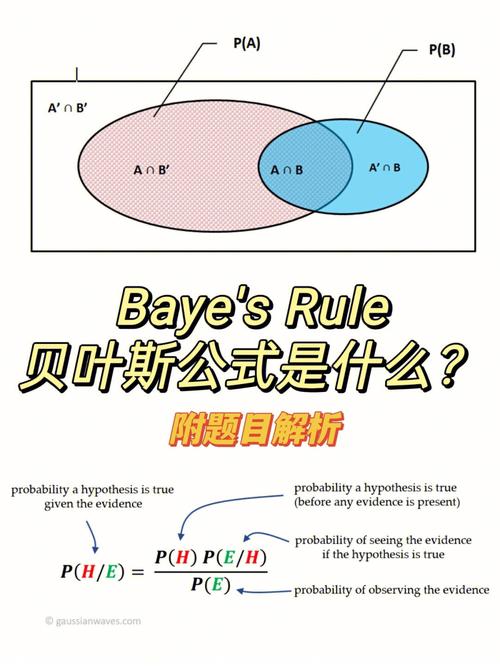
贝叶斯定理是贝叶斯模型的中心,它描绘了后验概率与先验概率之间的联系。其公式如下:
$$ P(A|B) = \\frac{P(B|A) \\cdot P(A)}{P(B)} $$
其间,$ P(A|B) $ 表明在事情B产生的条件下事情A产生的概率,$ P(B|A) $ 表明在事情A产生的条件下事情B产生的概率,$ P(A) $ 是事情A的先验概率,$ P(B) $ 是事情B的边沿概率。
二、先验概率与后验概率

在贝叶斯模型中,先验概率是指在未观察到任何依据之前,对某个事情产生的概率估量。然后验概率则是在观察到某些依据后,对某个事情产生的概率估量。经过贝叶斯定理,咱们能够依据先验概率和条件概率来核算后验概率。
三、条件概率与独立性假定
条件概率是指在某个条件下,另一个事情产生的概率。在贝叶斯模型中,咱们一般假定特征之间是条件独立的,即在给定类别的情况下,特征之间彼此独立。这一假定使得贝叶斯模型在处理高维数据时具有较好的功能。
四、朴素贝叶斯模型
朴素贝叶斯模型是一种依据贝叶斯定理的分类算法,它假定特征之间是条件独立的。朴素贝叶斯模型包含以下几种类型:
高斯朴素贝叶斯(Gaussian Naive Bayes):适用于接连特征。
伯努利朴素贝叶斯(Bernoulli Naive Bayes):适用于二分类数据。
多项式朴素贝叶斯(Multinomial Naive Bayes):适用于计数数据。
五、贝叶斯模型的使用场景
贝叶斯模型在以下场景中具有广泛的使用:
文本分类:如情感剖析、垃圾邮件过滤等。
医疗确诊:如疾病猜测、药物引荐等。
金融风控:如信誉评分、诈骗检测等。
图像辨认:如人脸辨认、物体检测等。
六、贝叶斯模型的优缺陷

贝叶斯模型具有以下长处:
简略易完成:贝叶斯模型的结构简略,易于了解和完成。
泛化能力强:贝叶斯模型在处理高维数据时具有较好的功能。
可解说性强:贝叶斯模型能够供给关于特征重要性的信息。
贝叶斯模型也存在以下缺陷:
核算杂乱度高:在处理大规模数据集时,贝叶斯模型的核算杂乱度较高。
对噪声灵敏:贝叶斯模型对噪声数据较为灵敏。
贝叶斯模型是机器学习中一种依据概率核算的强壮东西,尤其在分类和猜测使命中表现出色。本文介绍了贝叶斯定理、先验概率、后验概率、条件概率、朴素贝叶斯模型以及贝叶斯模型的使用场景和优缺陷。经过本文的介绍,读者能够更好地了解贝叶斯模型在机器学习中的使用。
未经允许不得转载:全栈博客园 » 机器学习贝叶斯模型,深化解析机器学习中的贝叶斯模型

 全栈博客园
全栈博客园 机器学习双非研讨生,砥砺前行,开放光辉
机器学习双非研讨生,砥砺前行,开放光辉 AI扩图,改造图画处理,拓宽视觉构思无限或许
AI扩图,改造图画处理,拓宽视觉构思无限或许 ai智能,未来科技浪潮中的引领者
ai智能,未来科技浪潮中的引领者 ai机器人打电话软件,重塑电销职业,进步营销功率
ai机器人打电话软件,重塑电销职业,进步营销功率 机器学习 医疗,机器学习在医疗范畴的使用与未来展望
机器学习 医疗,机器学习在医疗范畴的使用与未来展望 免费的ai作图软件,构思无限,轻松上手
免费的ai作图软件,构思无限,轻松上手 常用的机器学习算法,常用机器学习算法概述
常用的机器学习算法,常用机器学习算法概述











