好的，这里是一个简略的C言语程序，用于生成和打印杨辉三角：

```cinclude

define MAX_ROWS 10

// 函数用于核算组合数 Cint combination { if { return 1; } else { return combination combination; }}

// 主函数int main { int i, j;

// 打印杨辉三角 for { for { printfqwe2; } printf; }

return 0;}```

这个程序界说了一个名为 `combination` 的函数，它运用递归的方法来核算组合数 C。在 `main` 函数中，咱们运用两个嵌套的循环来生成和打印杨辉三角。外层循环操控行数，内层循环操控每行中的数字。

你能够将这段代码复制到C言语的编译器中，然后编译并运转它，以检查杨辉三角的输出。

浅显易懂C言语完成杨辉三角

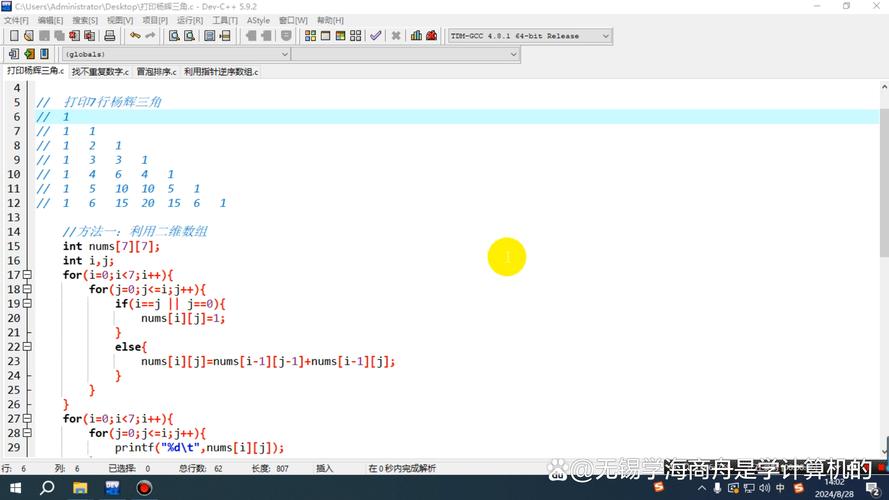
杨辉三角（Pascal's Triangle）是一种常见的数学图形，它由一系列数字组成，每一行的数字都是上一行相邻两个数字之和。杨辉三角在数学、核算机科学等范畴都有广泛的运用，如组合数学、概率论等。本文将具体介绍怎么运用C言语完成杨辉三角的打印。

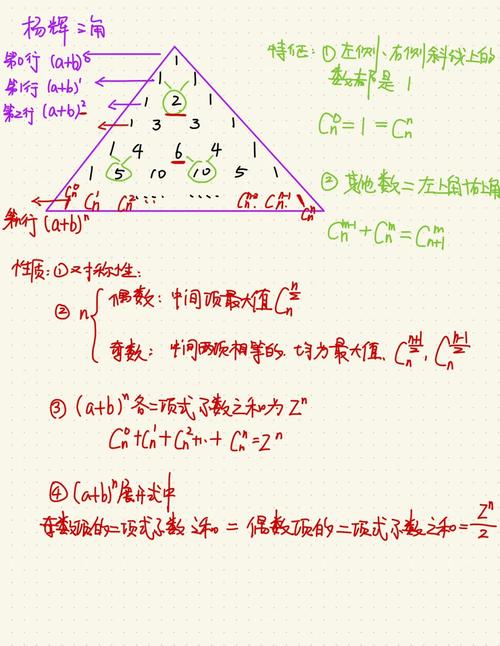
二、杨辉三角的基本原理

杨辉三角的每一行都对应于二项式定理的打开。例如，二项式定理中的(a b)^n能够打开为C(n,0)a^nb^0 C(n,1)a^(n-1)b^1 ... C(n,n)a^0b^n。其间，C(n,k)表明从n个不同元素中取出k个元素的组合数，也便是杨辉三角中第n行的第k 1个数。

三、C言语完成杨辉三角

下面是一个运用C言语完成的杨辉三角打印程序。该程序首要界说一个函数用于核算组合数，然后运用嵌套循环打印杨辉三角。

```c

include

// 函数：核算组合数

int combination(int n, int k) {

if (k == 0 || k == n) {

return 1;

}

return combination(n - 1, k - 1) combination(n - 1, k);

// 函数：打印杨辉三角

void printPascalTriangle(int n) {

int i, j;

for (i = 0; i < n; i ) {

// 打印空格

for (j = 0; j < n - i - 1; j ) {

printf(\

未经允许不得转载：全栈博客园 » 杨辉三角c言语程序,浅显易懂C言语完成杨辉三角