线性回归是计算学中一种十分根底和常用的办法,用于描绘两个变量之间的联系。在R言语中,线性回归能够经过`lm`函数完成。这个函数会树立一个线性模型,并回来模型的详细计算信息。
根本线性回归模型
假定咱们有两个变量:自变量(独立变量)X和因变量(依靠变量)Y。线性回归的意图是树立一个模型,用X来猜测Y。根本的线性回归模型能够表明为:
$$ Y = beta_0 beta_1X epsilon $$
其间,$beta_0$是截距,$beta_1$是斜率,$epsilon$是差错项。
R言语完成
在R中,咱们能够运用`lm`函数来拟合线性回归模型。例如,假如咱们有一个名为`data`的数据框,其间包括自变量`X`和因变量`Y`,咱们能够这样拟合模型:
```Rsummary```
示例
假定咱们有一个名为`data`的数据框,其间包括两个变量:`X`和`Y`。咱们能够这样拟合一个线性回归模型:
这个示例会创立一个线性回归模型,并用`summary`函数显现模型的计算信息,包括斜率、截距、R平方值等。
其他选项
`lm`函数还有许多其他选项,例如能够指定模型的其他参数,或许运用不同的回归办法(如加权最小二乘法)。更多详细信息能够参阅R言语的官方文档或相关书本。
以上是线性回归在R言语中的根本完成。假如你有更详细的问题或需求进一步的解说,请随时告诉我。
浅显易懂R言语线性回归:原理、运用与实例剖析
线性回归是计算学中一种常用的数据剖析办法,它经过树立一个线性模型来描绘因变量与自变量之间的联系。R言语作为一种功能强大的计算软件,供给了丰厚的线性回归剖析东西。本文将浅显易懂地介绍R言语线性回归的根本原理、运用场景以及实例剖析。
一、线性回归的根本原理
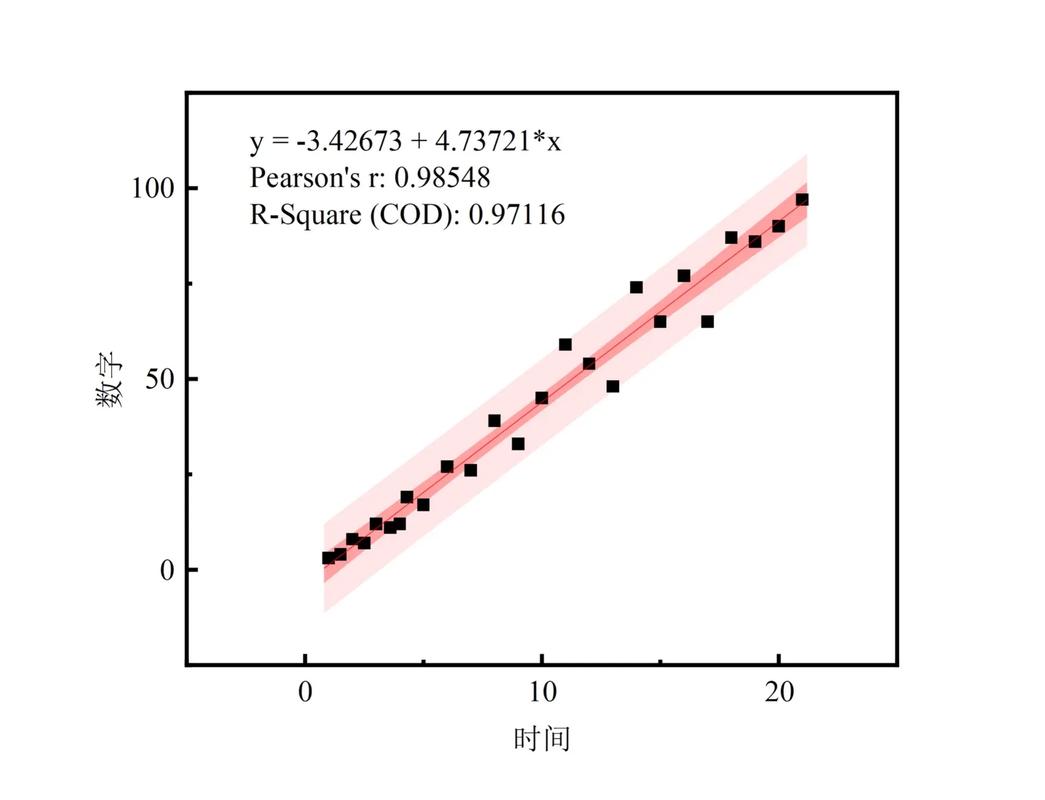
线性回归模型的根本形式为:Y = β0 β1X1 β2X2 ... βpXp ε,其间Y为因变量,X1, X2, ..., Xp为自变量,β0为截距,β1, β2, ..., βp为斜率,ε为差错项。
线性回归的意图是经过最小化差错项的平方和来估量模型参数β0, β1, ..., βp,然后树立最佳拟合的线性模型。
二、R言语线性回归剖析
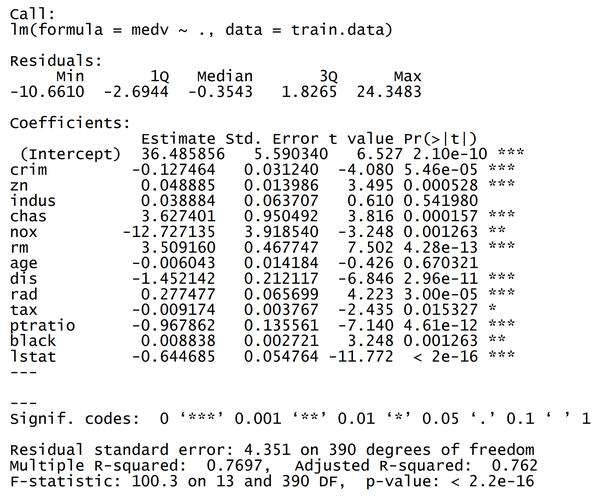
R言语供给了lm()函数用于拟合线性回归模型。以下是一个简略的线性回归实例:
在上面的代码中,Y为因变量,X1和X2为自变量,dataset为数据集。summary()函数用于输出模型的详细信息,包括系数估量、t值、p值等。
三、线性回归的运用场景
经济学:剖析经济增加、出资报答等。
医学:研讨疾病发生率、药物效果等。
生态学:剖析物种散布、环境要素等。
社会科学:研讨人口增加、教育水平等。
四、实例剖析
以下是一个运用R言语进行线性回归剖析的实例:
事例:剖析房价与面积、地段的联系
数据集:house_data.csv,包括以下字段:house_id(房子编号)、area(面积)、location(地段)、price(价格)。
library(readr)
data <- read_csv(\
未经允许不得转载:全栈博客园 » r言语线性回归,原理、运用与实例剖析

 全栈博客园
全栈博客园 c言语二进制怎样表明,二、什么是二进制
c言语二进制怎样表明,二、什么是二进制 c言语编程题经典100例
c言语编程题经典100例 c言语static,深化解析C言语中的static关键字
c言语static,深化解析C言语中的static关键字 python编译,从源码到可履行文件的全进程
python编译,从源码到可履行文件的全进程 python的运用范畴有哪些,二、Web运用开发
python的运用范畴有哪些,二、Web运用开发 python读取文件,python读取文件数据
python读取文件,python读取文件数据 go言语编译,Go言语 编译进程 编译优化 编程言语
go言语编译,Go言语 编译进程 编译优化 编程言语









