线性回归是机器学习中最根本的算法之一，用于猜测接连数值型输出。它假定输入特征和输出之间存在线性联系，即输出是输入特征的线性组合。线性回归的方针是找到最佳拟合直线，使得猜测值与实践值之间的差错最小。

线性回归能够分为两种类型：简略线性回归和多元线性回归。简略线性回归只要一个自变量和一个因变量，而多元线性回归有多个自变量和一个因变量。

线性回归的数学公式如下：

$$y = beta_0 beta_1x_1 beta_2x_2 cdots beta_nx_n$$

其间，$y$ 是因变量，$x_1, x_2, ldots, x_n$ 是自变量，$beta_0, beta_1, ldots, beta_n$ 是回归系数。

线性回归的回归系数能够经过最小二乘法进行估量。最小二乘法的方针是找到一组回归系数，使得猜测值与实践值之间的差错平方和最小。

线性回归的评价方针包含均方差错（MSE）、均方根差错（RMSE）和R平方（R2）。MSE和RMSE越小，模型的猜测作用越好；R2越挨近1，模型的拟合作用越好。

线性回归是一种简略而强壮的算法，广泛运用于各个领域，如经济学、金融学、生物学等。线性回归也有一些局限性，如它假定输入特征和输出之间存在线性联系，而实践上这种联系或许并不总是线性的。此外，线性回归对异常值和多重共线性灵敏，因此在实践运用中需要对这些状况进行处理。

除了线性回归，还有许多其他机器学习算法能够用于猜测接连数值型输出，如决策树、随机森林、支撑向量机等。这些算法在处理非线性联系和杂乱数据结构方面或许具有更好的功能。

机器学习线性回归剖析：原理、运用与完成

机器学习，线性回归，数据剖析，运用场景，Python完成

线性回归是机器学习中最根底且广泛运用的回归算法之一。它经过树立一个数学模型来描绘因变量与自变量之间的线性联系，然后完成对不知道数据的猜测。本文将具体介绍线性回归的根本原理、运用场景以及Python完成办法。

二、线性回归的根本原理

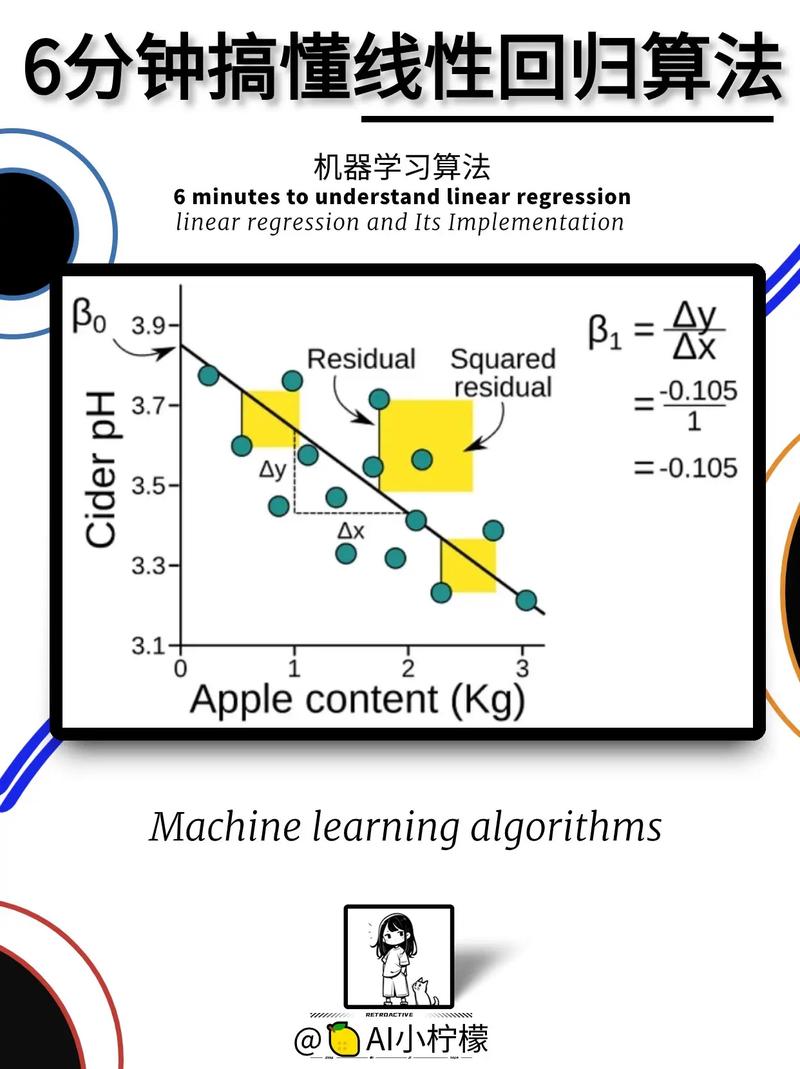
线性回归的方针是找到一个最佳拟合直线，使得猜测值与实在值之间的差错最小。在数学上，线性回归模型能够表明为：

其间，y 是方针变量（因变量），x 是自变量，β0 是截距，β1, β2, ..., βn 是自变量的系数，ε 是差错项。

线性回归模型经过最小化差错平方和来估量系数。常用的差错平方和公式为：

其间，n 是样本数量，yi 是第 i 个样本的实践值，?i 是第 i 个样本的猜测值。

三、线性回归的运用场景

房价猜测：依据房子面积、方位等特征来猜测房价。

股票市场：剖析股价与经济方针之间的线性联系。

医学研讨：剖析医治计划与患者恢复时刻之间的联系。

工业出产：猜测产品产量与出产设备参数之间的联系。

四、线性回归的Python完成

在Python中，咱们能够运用scikit-learn库来完成线性回归。以下是一个简略的线性回归完成示例：

import numpy as np

创立数据集

X = np.array([[1, 2], [2, 3], [3, 4], [4, 5]])

y = np.array([1, 2, 3, 4])

创立线性回归模型

练习模型

猜测

print(\

未经允许不得转载：全栈博客园 » 机器学习线性回归剖析,二、线性回归的根本原理